Oh, those family gatherings. Once you have stuffed yourself silly with an elaborate meal, there is little left to help you avoid spending some dreaded “quality time” with your relatives. Rather than fill an evening debating politics or dodging prying personal questions, many people turn to board games as a simple and polite way to avoid actually having to speak to each other — and for mathematicians Hannah Fry and Thomas Oléron Evans, there is nothing more magical than a full-blown family argument caused by a good old-fashioned game of Monopoly. Below, they explain how to win.

Officially, Monopoly ends when all players but one go bankrupt. In reality, it ends when your sister accuses one or all of you of cheating, flips the board across the room, and storms off in a shower of miniature plastic houses. Monopoly, whose sole objective is to have you force your friends and family into poverty, seems to have the ability to turn even the most angelic of us into a monster. But if you are going to be involved in a vicious fight with your family, you might as well emerge the victor.

The key to success in Monopoly is noticing that not all properties are created equal. This is where mathematics steps in to help. Knowing which sets are likely to give you better returns is your ticket to board-game glory, ensuring it’s you with the smug, satisfied smile on your face while your relatives weep into their ice cream bowls over their devastating defeat.

Ultimately, Monopoly is about money. So, to find the best strategy, we need to take into account how much you can expect each property, fully loaded with hotels, to earn for every roll of the dice and how much investment is required to get you there. To make a well-informed decision about which are the best properties to buy, you want to know how quickly you’ll make your money back and how quickly you’ll earn the big bucks once you do.

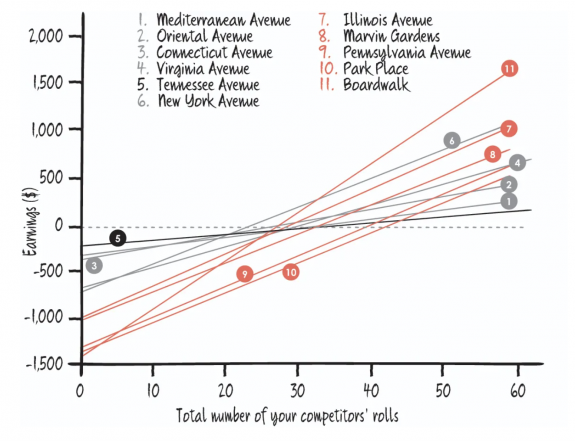
The below graph shows a selection of properties from each set. With a hotel on each, your earnings are shown up the vertical (y) axis and the total number of your competitors’ rolls along the horizontal (x) axis. Each property starts off with a negative value, as you have to invest in them to begin with; as soon as a property crosses the dotted line at zero the amount it’s earned in rent exceeds the amount it cost you. Anything else it earns is pure profit.

Of the properties you can build on, those from the brown and light blue sets start closest to the dotted line because they are so cheap to buy and build on. The slope of Mediterranean Avenue (line 1) is very shallow, meaning it takes a long time before it will start making money — and even when it does, you won’t make much. Oriental Avenue (line 2) does a lot better and is up there with the best-earning sets until about 25 rolls. New York Avenue (line 6), with its steep slope of $30 expected earnings per roll on the graph, is quickly into profit and holds on to the lead of the best-performing property until well over 30 throws. (In Monopolyland, unlike real life, the railroads are relatively affordable. However, very much like in real life, it’s unlikely they will get you anywhere fast.)

Boardwalk (line 11), however, is the standout property on the board. Despite starting way down on the y axis, it soon streaks into first place, and it stays there for the rest of time. If you can afford to buy and build on Boardwalk, it looks like it’s a winning strategy.

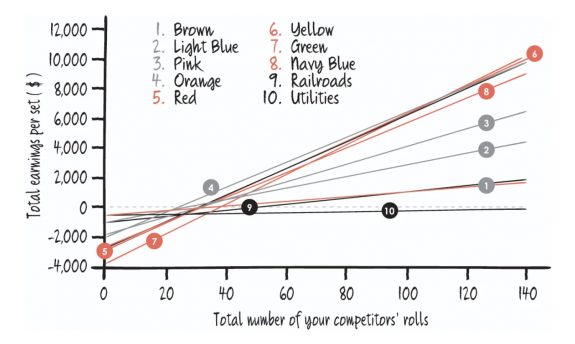
But Monopoly doesn’t let you build on single properties. If you plan on building any houses or hotels, you’ve got to invest in complete sets. And so the previous graph — although it demonstrates why so many people go for Boardwalk — doesn’t quite tell the whole story. For that, you’ve got to apply the same idea to the performance of complete sets.

This graph gives a more accurate picture and tells quite a different story.

Park Place, which is very expensive to buy and build on but is rarely visited, ends up dragging down the Boardwalk effect. The navy blue set also has two rather than three squares. This means it requires a smaller investment than the greens and so starts higher on the y axis — but it also means fewer opportunities to pull in the cash. So, dramatic as it might be when someone lands on Boardwalk, it’s just too rare an event to be worth the backing.

There is no single set that holds the key to winning the game. But there is always one set which will be the best for you to target — the secret to which lies in the x axis. At all times, you are looking to hold the property whose line is at the top of the pile, which changes depending on how long the game goes on.

Since the average game of Monopoly takes about 30 turns per competitor, the set you want will change depending on how many opponents you have. More opponents means more turns, and hence it makes more sense to put your money into longer-term investments. It’s also worth investigating the benefits of house buying and whether hotels really are the best buildings to aim for.

When playing against just one opponent, go for the orange or light blue sets (both if you can). The same is true in a game with more opponents, but only in the early stages. Then, in a game against two or three opponents which is likely to go on for a while, it’s orange and red that you want to be targeting. And if you have any more than three opponents, green becomes your best shot for a chance at success.

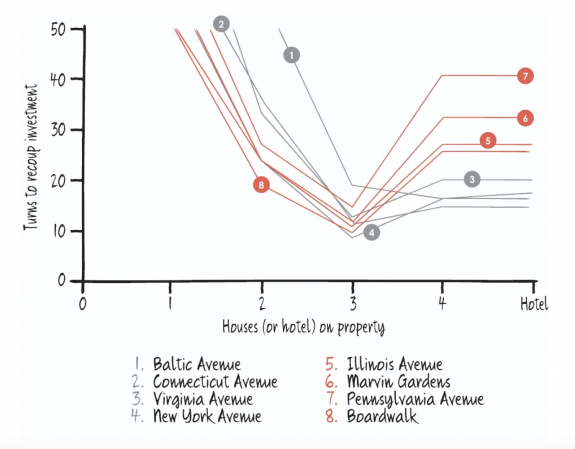
Eventually, any investment in Monopoly will make its money back, but early on in the game, should you invest in building — or hang on to the cash in case you find yourself on the receiving end of a big bill? You can compare these two scenarios, and look at how many rolls of the dice by your competitors it will take before you’re better off investing in that extra house.

In the below graph are the results for the best-performing property of each set when deciding to build 1, 2, 3 or 4 houses or a hotel. The lower the line on the y axis, the more quickly your property starts making you money. The first house takes a really long time to start paying for itself.

For every property (apart from the brown set — which, let’s be honest, is basically pointless), it’s the third house that is really worth investing in quickly. After that, build more if you have the money, but it’s probably worth waiting a few turns if cash is a bit tight. Since there are a limited number of houses in the game, building three houses on properties early and then waiting to upgrade further has the added advantage of potentially blocking the building projects of other players. Sneaky, huh?

But finally, if you take nothing else away from this entire story, remember this: Whatever way you look at it, utilities are completely pointless.

Adapted from the book The Indisputable Existence of Santa Claus: The Mathematics of Christmas by Hannah Fry and Thomas Oléron Evans. Copyright © 2016, 2017 by Dr. Hannah Fry and Dr. Thomas Oléron Evans. Published in 2017 by The Overlook Press, Peter Mayer Publishers, Inc. http://www.overlookpress.com. All rights reserved. This book is available at Amazon, Barnes and Noble, and Indiebound.

Featured art credit: Shutterstock.

Author bios: Hannah Fry is a mathematician at the University College London, where she uses mathematical models to study patterns in human behavior, from riots and terrorism to trade and shopping. Thomas Oléron Evans is a Research Associate at University College London, where he has been working on the ENFOLD-ing project, developing new tools for complexity science and modeling global trade, migration, aid and security. This piece was adapted for TED-Ed from this Ideas article.